Home

CV

Research

People

Teaching

Blog

Schmidt

- Noether Rules

....
-An external potential and the corresponding density profile. Mouse over to displace.

Overview. Noether's Theorem is familiar from a range of physics from Classical Mechanics to field theories such as General Relativity. In recent work, we show that the Theorem applies in an interesting and nontrivial way to Statistical Mechanics. Rather than the familiar correspondence of the underlying symmetries of a physical system with conservation laws, here we address thermal systems that are disordered on microscopic scales. The formlism allows to formulate force and torque sum rules ("Noether identities").

Graphics. The above illustrations show the external potential (left) and the density profile (right) of a confined fluid as a function of position. Mouse over the graphics in order to spatially shift to the right each function by a displacement vector. This spatial shift (horizontal arrow) induces a corresponding shift in the value of the respective function (vertical arrow). When considering the shifting operation for the underlying statistical objects, such as the partition sum, the free energy functional, in the case of dynamics the power functional, one can derive hierarchies of exact identities ("sum rules").

For an enaging description of the Noether Theorem in an elementary context of classical mechanics, see Toby Hendy's beautiful description on YouTube.

A popular talk (in German) can be found at ARD alpha.

Sophie's blog post about variances and invariances at physicscommunity.nature:
Variance of fluctuations from Noether invariance
Commun. Phys. 5, 276 (2022).

Update: Here is the quantum version :)
Force balance in thermal quantum many-body systems from Noether's theorem
J. Phys. A: Math. Theor. 55, 464003 (2022).

Dynamical Shifting. For the dynamics we consider three different types of spatial displacement ("shifting") operations. Mouse over the graphics below to see what each of them does.

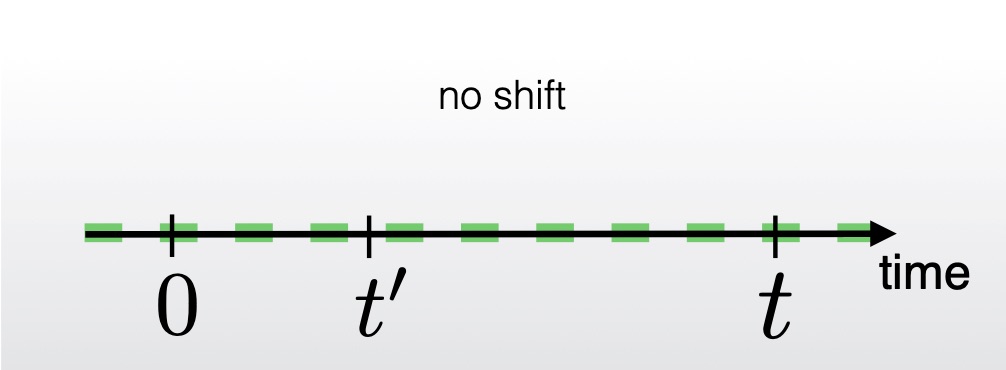
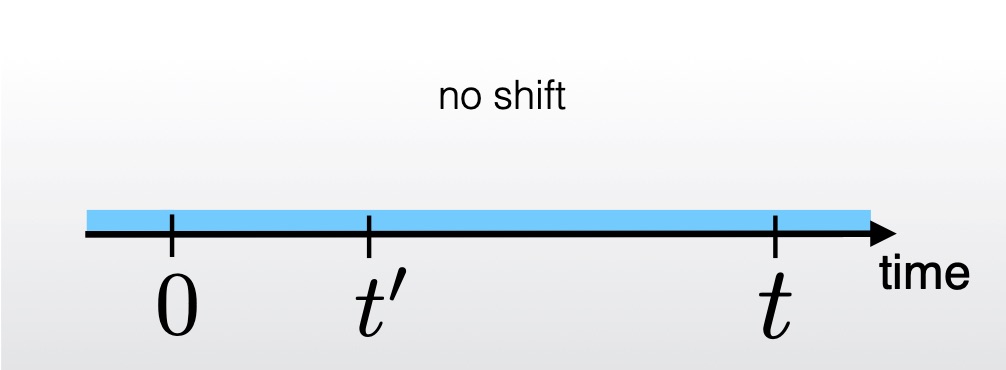
The power functional reacts differently to the different shifting operations, and one is able to formulate exact force sum rules (Noether identities) that are nonlocal in time, i.e. they couple the instantaneous state of the system with its past, a mechanism that is refered to as memory.

-Für Menschen mit Hintergrund-

Die Statistische Physik ist die Lehre des Zusammenwirkens von vielen Einzelbausteinen zu einem kollektiven Ganzen. Beispiele für Anwendungen sind: i) viele Wassermoleküle, die ein makroskopisches Ganzes wie beispielsweise einen See bilden, ii) Proteine oder andere gelöste (kolloidale) Teilchen in beispielsweise einem Glas Milch, oder iii) synthetisch hergestellte Janus-Teilchen, die sich selbst in einer Lösung fortbewegen können, wenn entsprechender Treibstoff zugesetzt wurde.

Weil solche Systeme typischerweise ungeordnet auf kleinen Skalen sind, ist eine statistische Beschreibung maßgeblich. Trotz der Unordnung entstehen klar identifizierbare makroskopische Eigenschaften, wie beispielsweise das zähe und viskose Flussverhalten einer langsam fließenden Flüssigkeit. Ein Verständnis solch makroskopischen Verhaltens zu erarbeiten, ausgehend von den zugrundeliegenden Kräften, welche zwischen den Molekülen (oder Kolloiden) wirken, ist eine zentrale Aufgabe und große Herausforderung in der Statistischen Physik.

Emmy Noethers Theorem ist üblicherweise in einem gänzlich anderen Teil der Physik beheimatet, nämlich dem der Zeitentwicklung von physikalischen Systemen. Dabei geht es neben Teilchen-basierten Systemen, wie den oben genannten Flüssigkeiten, auch um Feldtheorien wie Einsteins Allgemeiner Relativitätstheorie. Emmy Noether, als eine zentrale Gründungsfigur der modernen reinen Mathematik, hat früh in ihrer Karriere, kurz nach ihrer Promotion, ihr für die Physik überaus weitreichendes Theorem formuliert. (Es handelt sich um mehrere einzelne und verwandte Theoreme.)

Wie Physikstudenten (m/w/d!) bereits früh in ihrem Studium lernen, verbindet das Noether-Theorem die vorhandenen Symmetrien eines physikalischen Systems mit entsprechenden Erhaltungssätzen. Ein berühmtes Beispiel für diese Verbindung ist die Unempfindlichkeit (Invarianz) gegenüber Verschiebung im Raum mit der Impulserhaltung in der gleichen Richtung. Beispielsweise lassen sich Kufen auf Eis entlang deren Vorwärtsrichtung verschieben, was zu ungebremstem Weitergleiten führt. In der Realität jedoch kommt die Eisprinzessin durchaus zur Ruhe und gleitet nicht bis in alle Ewigkeit weiter. Dieser dissipative Vorgang passiert, weil reale Systeme Reibung zeigen und oft überaus ungeordnet auf kleinen (mikroskopischen) Skalen sind. Daher könnte man glauben, dass Noethers Theorem doch nicht wirklich für reale Systeme gilt.

In der in Communications Physics publizierten Arbeit zeigen wir, dass Noethers Argument durchaus so formuliert werden kann, dass es für Systeme mit Unordnung gilt. Dabei handelt es sich insbesondere um Systeme bei endlicher Temperatur, so dass neben der Energie die Entropie eine wesentliche Rolle spielt. Statt Erhaltungssätze auszudrücken, gelten die Noetherschen Aussagen in komplexen thermischen Systemen für Kräfte. Wegen der statistischen Beschreibung handelt es sich dabei um gemittelte Kräfte, welche realen Messwerten entsprechen. Ein Beispiel eines solchen Resultates ist eine Kraftregel, die besagt, dass die Summe aller internen Kräfte (also solche die beispielsweise Moleküle aufeinander ausüben) in der Summe verschwindet.

Dies impliziert, dass sich der Baron Münchhausen nicht an den eigenen Haaren aus dem Sumpf ziehen kann. -Die Gesamtkraft, die er auf sich selbst ausüben kann, ist Null. Wir zeigen, dass diese Unmöglichkeit sehr allgemein ist. Bestünde der Baron aus den oben genannten selbst schwimmenden ("aktiven") Teilchen, so würde ihm das auch nicht dabei helfen aus dem Sumpf zu kommen. Mit einer Reihe von mathematischen Techniken aus dem Gebiet der Variationsrechnung gewinnen wir allgemeine Aussagen über sogenannte Korrelationsfunktionen, die man verwendet, um Unordnung oder deren Abwesenheit, also Ordnung, systematisch zu quantifizieren.

Ein Kurzvortrag dazu im Fernsehen ist hier: ARD alpha.