A short overview of research topics is given in the following. The snapshot on the right is taken from a computer simulation of a mixture of hard spheres and hard rods that displays phase separation.
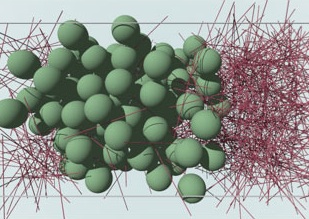
Colloidal rod-sphere mixture.
| Home | CV | Research | People | Teaching | Blog |
| Schmidt | - Statistical and Nonequilibrium Physics |
|
[bare list]
[illustrated]
[by topic]
Publons
A short overview of research topics is given in the following. The snapshot on the right is taken from a computer simulation of a mixture of hard spheres and hard rods that displays phase separation. |

Colloidal rod-sphere mixture. |