| 46. |
Replica density functional study of one-dimensional
hard core fluids in porous media H. Reich and M. Schmidt, J. Stat. Phys. 116, 1683 (2004). Locate in [bare] [illustrated] list. Get [full paper] as pdf. Extract. A binary quenched-annealed hard core mixture is considered in one dimension. Two different density functional approaches are employed: The first approach uses Percus' functional for the annealed component and an explicit averaging over matrix configurations; this is numerically exact. The second approach is based on a quenched-annealed density functional whose results we find to approximate very well those of the former. Furthermore we give a derivation of the underlying replica density functional theory. [more] 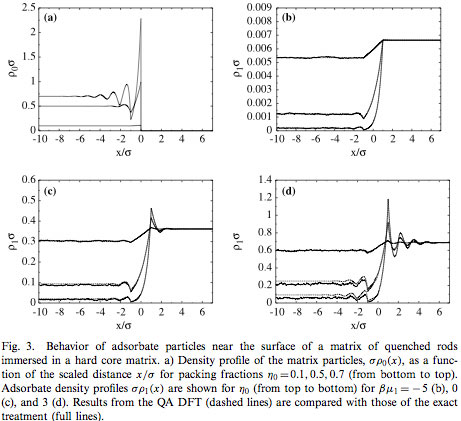 Read the [full paper] as pdf. |
Fluid interfaces
Colloid-polymer mixtures display fluid-fluid interfaces [21] [44], relevant for laser-induced condensation [35], capillary condensation [43] and evaporation [48], immersion in porous media [41], the appearance of the floating liquid phase [52], the competition between sedimentation and phase coexistence [51], tension at a substrate [45], the experimental observation of thermal capillary waves [47], and the contact angle of the liquid-gas interface and a wall [50]. In colloidal rod-sphere mixtures fluid-fluid interfaces were investigated with theory [30] and simulation [42]. Hard sphere fluids were considered at surfaces of porous media [37], in random fiber networks [39], and in one dimensional cases [46].Fluids in random media
The density functional theory for quenched-annealed mixtures [24] relates the quenched components to a random porous medium and the annealed components model to an adsorbate fluid (mixture). See [46] for the explicit relation to the the replica trick. Colloid-polymer mixtures were studied in bulk random matrices [32], exhibiting (gas-liquid) interfaces [41], and wetting properties at porous substrates [56]. Rods were immersed in quenched sphere matrices [54], and spheres were immersed in random fibre networks [39]. Freezing is hindered in the presence of disorder [38]. See [33] for the related non-equilibrium process of random sequential adsorption.[more]